I fully appreciate this is hardly the right time of year to be worrying about this sort of thing, but you'll be thanking me in December, mark my words.
Have you ever noticed how the year number changes at the end of each year? Damned confusing. Well, I've been doing some reverse-engineering, and I've come up with a handy, little formula for working out what next year's number will be:
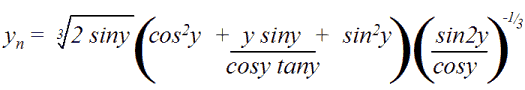
(Where yn = next year's number, and y = the current year's number. Works for all years after 1 A.D.)
I await the call of the Nobel Committee.
You should await the call of the men in white coats!
I'm surprised nobody has asked what happens if cosy or tany is zero, thereby leading to a division-by-zero error.
Evidently, you are better mathematicians than I gave you credit for, and have realised that y is measured in radians, and not degrees, and is an integer - so the odds of such an error are miniscule in the extreme.
The zeros of cos y are at(pi/2 + y*pi). The zeros of tan are at y*pi, so not only are the odds miniscule, it cant happen. Most fantastically pointless formula for a long time, I salute you Richard.
Thanks. My miniscule in the extreme comment was intended as a dry/wry understatement, what with pi being irrational and year numbers being integers and everything.
Pi is not only irrational but transcendental, and yet
π = (4/1) – (4/3) + (4/5) – (4/7) + ...
so your formula is not that implausible. You didn't specify which cube root, though.
How about this one: yn+1 = yn – eiπ. Two transcendental numbers and an imaginary one, and no need to remember those pesky trig formulas.
One small request: “minuscule”, please, not “miniscule”.
I very nearly used Euler's magical eiπ as part of my original formula, but decided that might complicate matters a bit too much.
Minuscule eh? I didn't believe a word of it, of course, until I looked it up, and discovered you to be correct.